Нумерология
Нумерологическая классификация Алфавита
(открытая проблема)| № п/п |
NU №№ п/п |
БУКВА |
Сумма Прироста По №№ |
Сумма прироста NU №№ |
NU Сумм прироста NU №№ |
Параметр
1 |
Параметр 2 |
Параметр
3 |
Параметр
4 |
Параметр
5 |
Параметр
6 |
| 1 | 1 | А | 1 | 1 | 1 |
| 2 | 2 | Б | 3 | 3 | 3 |
| 3 | 3 | В | 6 | 6 | 6 |
| 4 | 4 | Г | 10 | 10 | 1 |
| 5 | 5 | Д | 15 | 15 | 6 |
| 6 | 6 | Е | 21 | 21 | 3 |
| 7 | 7 | Ё | 28 | 28 | 1 |
| 8 | 8 | Ж | 36 | 36 | 9 |
| 9 | 9 | З | 45 | 45 | 9 |
| 10 | 1 | И | 55 | 46 | 1 |
| 11 | 2 | Й | 66 | 48 | 3 |
| 12 | 3 | К | 78 | 51 | 6 |
| 13 | 4 | Л | 91 | 55 | 1 |
| 14 | 5 | М | 105 | 60 | 6 |
| 15 | 6 | Н | 120 | 66 | 3 |
| 16 | 7 | О | 136 | 73 | 1 |
| 17 | 8 | П | 153 | 81 | 9 |
| 18 | 9 | Р | 171 | 90 | 9 |
| 19 | 1 | С | 190 | 91 | 1 |
| 20 | 2 | Т | 210 | 93 | 3 |
| 21 | 3 | У | 231 | 96 | 6 |
| 22 | 4 | Ф | 253 | 100 | 1 |
| 23 | 5 | Х | 276 | 105 | 6 |
| 24 | 6 | Ц | 300 | 111 | 3 |
| 25 | 7 | Ч | 325 | 118 | 1 |
| 26 | 8 | Ш | 351 | 126 | 9 |
| 27 | 9 | Щ | 378 | 135 | 9 |
| 28 | 1 | Ъ | 406 | 136 | 1 |
| 29 | 2 | Ы | 435 | 138 | 3 |
| 30 | 3 | Ь | 465 | 141 | 6 |
| 31 | 4 | Э | 496 | 145 | 1 |
| 32 | 5 | Ю | 528 | 150 | 6 |
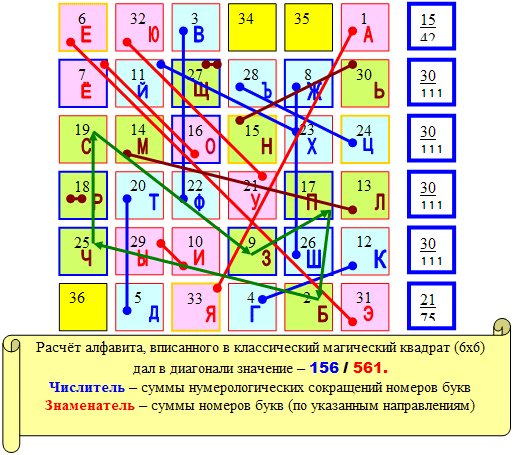
| 33 | 6 | Я | 561 | 156 | 3 |
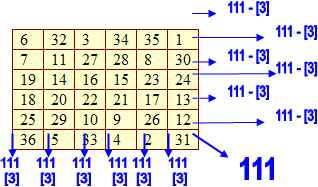
| ИТОГО: | 561 | 156 | {137} - {11} - [2] |
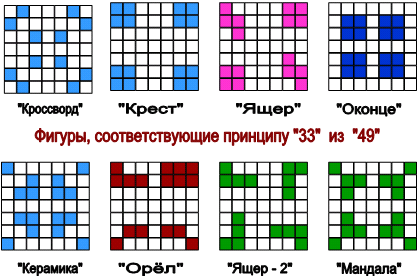
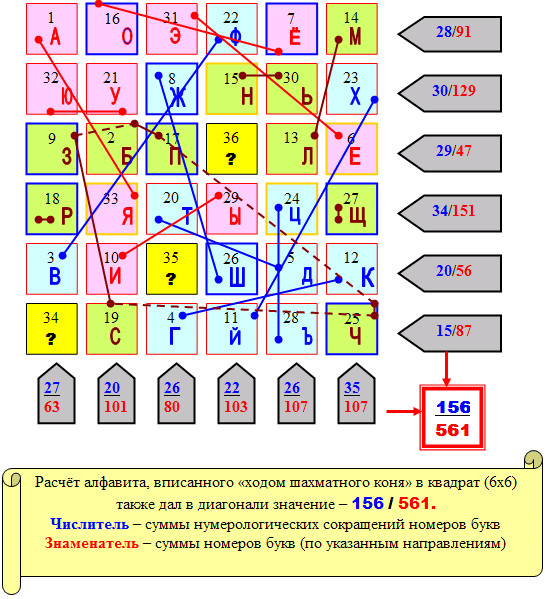
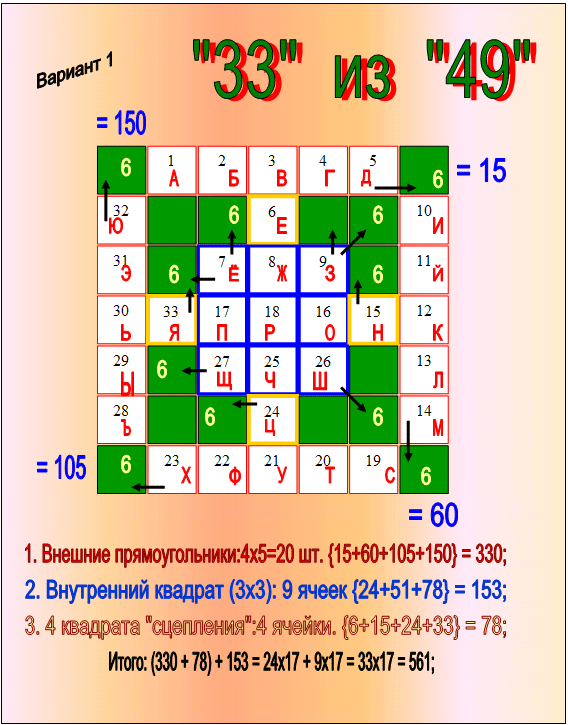
Русский алфавит (33 буквы) размещается в квадрате 7х7=49
1. (49 - 16) = 33;
2. (16 : 4) = 4;
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
ПРОЦЕДУРА «SP» для исследования
свойств натурального ряда чисел
(в частности, чисел алфавитного ряда)
Данная процедура вообще то была придумана для получения одних чисел из других чисел путём специальной операции, состоящей из двух действий.
Формально не имеется никакой логики в том, как и чем именно обосновывается данная процедура. Однако, как ни странно, но эта процедура – РАБОТАЕТ, а в эзотерических исследованиях этот смысл вполне может проявиться, в чём мы далее и попытаемся убедиться.
А пока – о самой процедуре.
Объектом преобразования обычно бывают числа, в большинстве случаев промежуточные числа т.н. нумерологических сокращений, которые мы обозначаем числами в фигурных скобках (например {57}).
Идея Метода (процедуры) S.P.такова:
1).Число (обычно двузначные) формально делится на две части:
Например: 57 – это «5» и «7».
2). Теперь эти части а) СКЛАДЫВАЮТСЯ (S) и б) ПЕРЕМНОЖАЮТСЯ (P)
Полученные результаты ПЕРЕМНОЖЕНИЯ (числа) нумерологически сокращаются до цифр.
Цифра от СЛОЖЕНИЯ – будет первой, а от УМНОЖЕНИЯ – второй.
На нашем примере это будет выглядеть так:
(S): :5+7 = {12} -- [3];
(P): 5 x 7 = {35} – [8];
В итоге имеем: НОВОЕ число -- 38.
57 --- трансформировалось --- в 38!
Вот и всё!
Условная формула этого преобразования представлена на рисунке ниже:
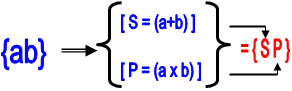 |
А теперь проверим с помощью этого метода (Процедуры SP) наш русский алфавит!
Точнее, не сам алфавит, а числа натурального ряда, служащие порядковыми номерами букв алфавита.
Оказывается, эта новая процедура позволяет вскрыть некую скрытую математическую закономерность внутреннего устройства и строения, которая, возможно, имеет отношение и к эзотерической сущности нашего алфавита.
Предвосхищая результаты, могу сказать, что данный метод оказался пригодным для поставленной задачи и, более того, продемонстрировал неизвестные ранее аномалии в строгой системе чисел натурального ряда чисел.
В таблице, рассчитанной ниже, можно увидеть прекрасные и чёткие закономерности, вскрываемые процедурой SP, которые резко нарушаются начиная с числа «25» (или - с буквы «Ч» по букву «Ы»), а затем, с числа «30» (буква «Ь») система вновь «восстанавливается», что подтверждает простым математическим расчётом.
Итак, смотрим нашу таблицу:
| Буквы | [S]:
суммацифр буквы |
[P]:
произведение цифрбуквы |
{ SP } |
№ буквы п/п |
К = (SP-№) |
Формула для букв | |
| А | 0+1 = 1 | 0х1 = 0 | 10 | 01 | 10-1=9 | 9х1=9 | |
| Б | 0+2 = 2 | 0х2 = 0 | 20 | 02 | 20-2=18 | 9х2=18 | |
| В | 0+3 = 3 | 0х3 = 0 | 30 | 03 | 30-3=27 | 9х3=27 | |
| Г | 0+4 = 4 | 0х4 = 0 | 40 | 04 | 40-4=36 | 9х4=36 | |
| Д | 0+5 = 5 | 0х5 = 0 | 50 | 05 | 50-5=45 | 9х5=45 | |
| Е | 0+6 = 6 | 0х6 = 0 | 60 | 06 | 60-6=54 | 9х6=54 | |
| Ё | 0+7 = 7 | 0х7 = 0 | 70 | 07 | 70-7=63 | 9х7=63 | |
| Ж | 0+8 = 8 | 0х8 = 0 | 80 | 08 | 80-8=72 | 9х8=54 | |
| З | 0+9 = 9 | 0х9 = 0 | 90 | 09 | 90-9=81 | 9х9=81 | |
| И | 1+0 = 1 | 1х0 = 0 | 10 | 10 | 10-10=0 | 10х0= 0 | |
| Й | 1+1 = 2 | 1х1 = 1 | 21 | 11 | 21-11=10 | 10х1=10 | |
| К | 1+2 = 3 | 1х2 = 2 | 32 | 12 | 32-12=20 | 10х2=20 | |
| Л | 1+3 = 4 | 1х3 = 3 | 43 | 13 | 43-13=30 | 10х3=30 | |
| М | 1+4 = 5 | 1х4 = 4 | 54 | 14 | 54-14=40 | 10х4=40 | |
| Н | 1+5 = 6 | 1х5 = 5 | 65 | 15 | 65-15=50 | 10х5=50 | |
| О | 1+6= 7 | 1х6 = 6 | 76 | 16 | 76-16=60 | 10х6=60 | |
| П | 1+7 = 8 | 1х7 = 7 | 87 | 17 | 87-17=70 | 10х7=70 | |
| Р | 1+8 = 9 | 1х8 = 8 | 98 | 18 | 98-18=80 | 10х8=80 | |
| С | 1+9 = 10 [1] | 1х9 = 9 | 109 | 19 | 109-19=90 | 10х9=90 | |
| Т | 2+0 = 2 | 2х0 = 0 | 20 | 20 | 20-20=0 | 0 х 11= 0 | |
| У | 2+1 = 3 | 2х1 = 2 | 32 | 21 | 32-21=11 | 1х {11}=11 | |
| Ф | 2+2 = 4 | 2х2 = 4 | 44 | 22 | 44-22=22 | 2х {11}=22 | |
| Х | 2+3 = 5 | 2х3 = 6 | 56 | 23 | 56-23=33 | 3х {11}=33 | |
| Ц | 2+4 = 6 | 2х4 = 8 | 68 | 24 | 68-24=44 | 4х {11}=44 | |
| Ч | 2+5 = 7 | 2х5 = 10 [1] | 71 | 25 | 71-25 = 46 (?) | 2х {23} | |
| Ш | 2+6 = 8 | 2x6 =12 [3] | 83 | 26 | 83-26 = 57 (?) | 3х (19} | |
| Щ | 2+7 = 9 | 2х7 = 14 [5] | 95 | 27 | 95-27 = 68 (?) | 4x {17} | |
| Ъ | 2+8 =10 [1] | 2x8 = 16 [7] | 107 | 28 | 107-28 =79 (?) | 1х {79} | |
| Ы | 2+9 = 11 [2] | 2x9 = 18 [9] | 119 | 29 | 119-29 =90 (?) | == ??? == | |
| Ь | 3+0 =3 | 3x0 = 0 | 30 | 30 | 30-30=0 | 0 х 12= 0 | |
| Э | 3+1 = 4 | 3x1 = 3 | 43 | 31 | 43-31=12 | 1х 12=12 | |
| Ю | 3+2 = 5 | 3x2 = 6 | 56 | 32 | 56-32=24 | 2х 12=24 | |
| Я | 3+3 = 6 | 3x3 = 9 | 69 | 33 | 69-33=36 | 3х 12=36 | |
| (!) | Далее попробуем вести расчёты (в порядке эксперимента) для неизвестных букв | ||||||
| Х1 | 3+4 =7 | 3х7=21(3) | 73 | 25(?) | 73-25=48 | 4х 12=48 | |
| Х2 | 3+5=8 | 3х5=15(6) | 86 | 26(?) | 86-26=60 | 5х 12=60 | |
| Х3 | 3+6=9 | 3х6=18(9) | 99 | 27(?) | 99-27=72 | 6х 12=72 | |
| Х4 | 3+7=10(1) | 3х7=21(3) | 103 | 19(?) | 103-19=84 | 7х 12=84 | |
| Х5 | 3+8=11(2) | 3х8=24(6) | 116 | 20(?) | 116-20=96 | 8х 12=96 | |
| Х6 | 3+9=12(3) | 3х9=27(9) | 129 | 21(?) | 129-21=108 | 9х 12=108 | |
| Х7 | 4+0=4 | 4х0=0 | 40 | 40 | 40-40=0 | 0=13х0 | |
| Х8 | 4+1=5 | 4х1=1 | 51 | 38 | 51-13=38 | 13=13х1 | |
| Х9 | 4+2=6 | 4х2=8 | 68 | 42 | 68-26=42 | 26=13х2 | |
| Х10 | 4+3=7 | 4х3=12=3 | 73 | 34 | 73-39=34 | 39=13х3 | |
| Х11 | 4+4=8 | 4х4=16=7 | 87 | 35 | 87-52=35 | 52=13х4 | |
| Х12 | 4+5=9 | 4х5=20=2 | 92 | 31 | 96-31=65 | 65=13х5 | |
| Х13 | 4+6=10 | 4х6=24=6 | 106 | 28 | 106-28=78 | 78=13х6 | |
| Х15 | 4+7=11 | 4х7=28=10=1 | 111 | 20 | 111-20=91 | 91=13х7 | |
| Х16 | 4+8=12 | 4х8=32=5 | 125 | 21 | 125-21=104 | 104=13х8 | |
| Х17 | 4+9=13 | 4х9=36=9 | 139 | 22 | 139-22=117 | 117=13х9 | |
| [S] -сумма | [P] – произв. | {S.P.} | № п/п | (SP - №) | Формула | ||
Таким образом, рассчитав таблицу вплоть до числа «49», мы видим, что СБОИ СЧЁТА происходят именно там, где это было отмечено ранее, а именно с числа «25».
Мы также видим, что если принять Метод S.P. за ПРАВИЛЬНЫЙ метод, то тогда на НЕКОТОРЫЕ номера натурального ряда будут «претендовать» несколько связываемых с ними букв, а некоторые номера останутся …СВОБОДНЫМИ(!?).
Это иллюстрирует специальная таблица (см. ниже):
Красным цветом выделены числа, где Метод S.P. даёт строго однозначный результат и месту может быть приписана только ОДНА БУКВА, имеющая формулу для своей «прописки» по этому месту в натуральном ряду чисел.
Синим цветом выделены те порядковые числа натурального ряда ( в пределах до числа 33), где «система законной прописки» даёт сбои (не работает )
Кроме того, в таблице показаны и данные о «буквах», которые претендуют на «чужие» места, а также НЕ ИСПОЛЬЗУЕМЫЕ места натурального ряда - отмечены знаком вопроса (?).
| 1А | 2Б | 3В | 4Г | 5Д | 6Е | 7Ё |
| 8Ж | 9З | 10И | 11Й | 12К | 13Л | 14М |
| 15Н | 16О | 17П | 18Р | 19С, Х4 | 20Т,(Х15), (Х5) | 21У (Х16) , (Х6) |
| 22Ф (Х17) | 23Х | 24Ц | 25Ч, (Х1) | 26Ш, (Х2) | 27Щ, (Х3) | 28Ъ, (Х13) |
| 29Ы | 30Ь | 31Э Х12 | 32Ю | 33Я | 34 (Х10) | 35 (Х11) |
| 36_ ?_ | 37_ ?_ | 38 (Х8) | 39_ ?_ | 40 (Х7) | 41 _ ?_ | 42 (Х9) |
| 43_ ?_ | 44_ ?_ | 45_ ?_ | 46_ ?_ | 47_ ?_ | 48_ ?_ | 49_ ?_ |
Анализируя таблицу далее, нетрудно увидеть, что СБОЙ наступает ПОСЛЕ 24-й буквы, что с математической точки зрения совершенно НЕОБЪЯСНИМО!
И хотя к алфавиту, (я повторяюсь!) строго говоря, исследование методом S.P. чисел натурального ряда НЕ ИМЕЮТ, существуют ДРУГИЕ ДОВОДЫ, которые дают основания для того, чтобы искать связи систем натурального ряда и алфавита.
По крайней мере, мне с полной достоверностью известно, что русский алфавит ранее неоднократно сокращался, в целом - не менее чем на 5 букв (которых, возможно, и не хватает для полной системы!).
Также, вполне возможно, что буквы Ч, Ш, Щ, Ъ, Ы (5 шт.) – находятся НЕ НА СВОЁМ (ПЕРВОНАЧАЛЬНОМ) МЕСТЕ, так как именно с этих номеров букв алфавита начинается СБОЙ и разрушается строгая математическая стройность всей системы, проверяемой методом S.P.
Как бы то ни было, но Метод S.P. – просто формальная математическая процедура, которой должны подчиняться ВСЕ ЧИСЛА натурального ряда, а этого как раз и не происходит!
Следуя формальной логике, мы должны были бы УТВЕРЖДАТЬ, что математическая система натурального ряда ОГРАНИЧЕНА только 24-мя числами. Но, ведь это - абсурд!
Значит, имеет право на существование ещё один вариант разрешения вскрытого противоречия – наличие неизвестной пока ещё ДРУГОЙ процедуры (Метода), где такие СБОИ при исследованиях на числах натурального ряда не происходят!
Короче говоря, вопрос остаётся открытым!